Public channels provide much of Slack’s advantages over email: they are searchable, long-lasting, themed conversations that are easy to join and leave. But for users, curating the perfect set of channels can leave them feeling like Goldilocks — it’s easy to be in too many, too few, or miss critical ones.
A common customer request is for tools to help curate channels as companies grow from 100 to 1,000 to 10,000 people using Slack. This is what motivated us to work on channel recommendations: how can we help users tune their channel list to make staying on top of Slack as easy as possible? This feature is one of the first major initiatives from the newly formed Search, Learning and Intelligence group based in NYC.
The Problem
Building a channel recommendation system can be seen as an application of recommender systems. Similar to a movie recommendation service, we want to recommend to users the channels we think are most relevant to them, surfacing these recommendations through Slackbot:

But what does it mean for a channel to be relevant? Unfortunately, there is no easy way to directly measure relevancy, but after trying a few different proxy metrics, we ultimately settled on an approximation of time spent in channel based on read and write activity. To compute these scores, we built a Spark pipeline that ingests read and write log data stored in the Hive data warehouse maintained by our amazing data engineering team and, for each team, outputs a matrix of user-channel activity where each row corresponds to a channel, each column corresponds to a user and each entry corresponds to our computed activity score.
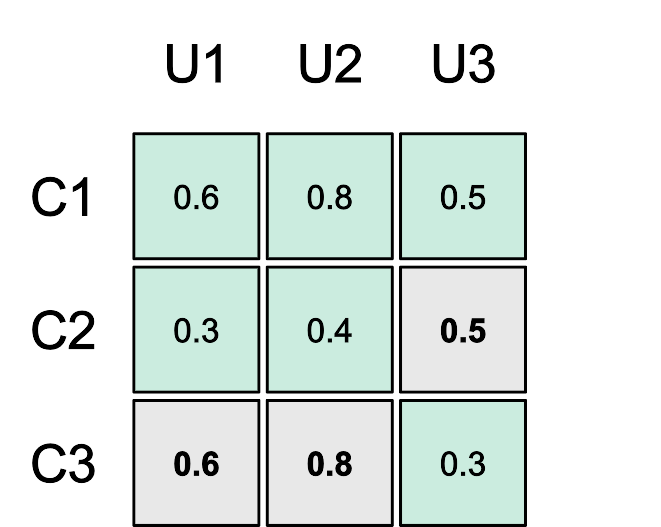
As a simple example, take a team with three users U1, U2 and U3 and three channels C1, C2 and C3. In reality, we deal with thousands of much larger matrices, each with entries numbering up to the millions, but the concepts are the same. Our example team user-channel activity matrix might look like this:

In the figure above, empty entries correspond to user-channel pairs where the user is not a member of the channel and filled entries correspond to the observed activity scores for user-channel pairs where the user is a member of the channel. Since we want to recommend to the user channels to join where we expect them to be the most active, we want to be able to predict what the activity score would be if the user were to join channels for which we have no observed score. The problem of generating channel recommendations thus becomes the problem of filling in the blank in each team activity matrix and recommending the highest predicted values for each user.
To evaluate our solution, we built a test set from a random subset of the filled entries. We also include a random sample of the empty cells in the set, setting their activity level to zero. This technique, drawn from One-Class Collaborative Filtering, models both the possibility that the user might not be in the channel because they are not aware of it, or that they just may not be interested in it. We can then evaluate our solution by computing a number of metrics, such as root-mean-square error or RMSE, between our predicted activity levels and the observed activity levels in our test set.
Similar Channels
We chose to approach this problem by first looking at similarities between channels. This is often referred to as item-based or item-item collaborative filtering in the literature.
For each team, we first compute a similarity score for each channel pair using cosine similarity between their activity rows. Given this similarity measure, channels with subsets of similarly active users are considered highly similar while channels with disjoint subsets of active users have a similarity of zero. It also has the interesting property of being scale invariant, which is important for this problem, since groups of users within a larger team often share a set of channels, each with a different average activity level.
Going back to our example team, to compute the similarity between C1 and C2, we first extract the rows for each channel.

We then compute the cosine similarity between the two.

We repeat this operation for each channel pair in the team to compute the full channel similarity matrix.

Nearest Neighbors
Now that we have a measure of similarity between each channel pair in the team, we can use that information to fill our original matrix. To do so, we use k-Nearest Neighbors (KNN) regression. That is, for a given user U and channel C, we lookup the k channels that are the most similar to C according to our channel similarity matrix. We then perform a weighted average of the activity scores between each of the top k similar channels and the user U.
For example, assuming k=2, to compute how relevant C2 is to U3, we first look at the C2 row in the similarity matrix. In this case, the k most similar channels, excluding C2 itself, are C1 and C3 with similarities of 0.89 and 0.0 respectively. We then lookup U3’s activity scores for C1 and C3 in our original activity matrix. In this case, the scores are 0.5 and 0.3. We can then compute the weighted average of the scores given the similarities.

We would thus expect U3 to have a 0.5 activity score in C2. We can then repeat the same approach to fill the remaining blank spaces in our original matrix.
Activity Transforms
The approach described above performs well on our test set, but we can do better. Going back to our original matrix, because of the scale invariance of cosine similarity, C1 and C2 are considered to be highly similar even though U1 and U2 are half as active in C2 as in C1. When computing U3’s predicted activity score for C2, we did not take this difference in scale into account. This likely leads us to overestimate U3’s predicted activity level in C2.
To mitigate this issue, we not only compute a similarity score between every pair of channels, but we also learn a linear relationship between activity levels in each channel. To do so, we look at the activity scores for the common set of members between the two channels and run a linear least squares regression using the scores for the first channel as input and the scores for the second as output. The result is a function of the form Ay = α ∙ Ax + β which can be used to transform an activity score in channel Cx to an expected activity score in channel Cy.
Going back to C1 and C2, the set of common users for these channels is U1 and U2.

In this case, the output of the least squares regression from activity in C1 to activity in C2 is:

If we were to repeat this process to learn a transform from activity in C1 to activity in C3, we would run into an issue: the system is underdetermined and there is an infinite number of solutions since C1 and C3 only share one common user. To get around this issue we introduce a fake data point in the regression with zero input and output.

In this case, the output of the least squares regression is:

Once we are done computing the activity transforms for every channel pair, we can apply them to the predicted activity levels in our KNN regression. Going back to our prediction for U3’s activity level in C2, we modify the weighted average to take the activity transforms into account.

This new estimate is much closer to the activity level of other users in C2 than our previous estimate.

In fact, by using this simple tweak, we were able to reduce the RMSE on our test set by an additional 35%!
But There’s More
In the end, a Machine Learning model does not make a product feature. In addition to improving the quality of the recommendations, we worked on their presentation. This included building out the infrastructure to index and serve the recommendations, choosing the wording and interaction model used by Slackbot and devising a triggering logic to push the final result in a way that wouldn’t seem too disruptive. Finally, to control the roll out as well as to quantify the success of the feature, we leveraged Slack’s internal experiment and logging systems. After releasing the feature to only 10% of teams, we already measured a 22% click-through rate for these recommendations.
But this is really just the start. We are already working on a larger regression model that leverages the work described above as well as other features to generate better recommendations. As we get more insight from usage of the feature, we hope to be able to continuously improve the quality of the recommendations we provide and, at the same time, we hope to make the work lives of our users simpler, more pleasant and more productive.
If you want to help us tackle data-driven product development challenges and help make the work life of millions of people simpler, more pleasant and more productive, check out our SLI job openings and apply today.








